4.1 Special Simplification

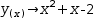
Integrals and derivatives are transformed by special simplification. As an example, consider these three function definitions

y(x)→x^2+x-2

(1)

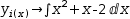
y_i(x)→∫x^2+x-2 ⅆx

(2)

y_d(x)→ⅆx^2+x-2ⅆx

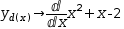
(3)

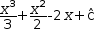
To integrate, select the integral in (2) and Simplify . If it can be integrated, the expression is replaced by the integral, in this case, x^3÷3+x^2÷2-2⋅x+ĉ. Note the constant of integration. It can be transformed to 0 by special simplification and, because it is always an addend, removed by algebraic simplification.

Similarly, select the derivative in (3) and Simplify . If it can be differentiated, the expression is replaced by the derivative: 2⋅x+1.

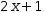
Other integration techniques are discussed in §4.4.